Correction du Bac blanc 2006: STI Génie mécanique
Partie A:
I: Fonctionnement à vide :
1) f = n.p = 25x 6 = 150 Hz
2) Tant que l'excitation reste constante l'alternateur fonctionne à flux constant ( c'est le courant d'excitation qui produit le flux inducteur).
3) on a EV=K.N.n.p.Φmax
K : constante de Kapp
N: Nombre de conducteurs de l'induit : c'est un paramètre constant.
p: nombre de paires de pôles reste constant
Φmax: le flux maximal sous un pôle reste constant tant que l'excitation est constante.
On peut alors regrouper ces quatre constantes dans une constante k tel que : k =K.N.p.Φmax 
EV = k.n
II:Fonctionnement en charge
1) Si n = 25 tr/s, et puisque l'excitation reste constante EV = 20 V .(voir l'énoncé on a bien mesuré la f.ém à vide pour n = 25 tr/s)
2) Uxs = Xs.I = 1.57 x 8 =12,56 V.
3) La loi des mailles nous permet d'écrire : 
v = 
xs + 
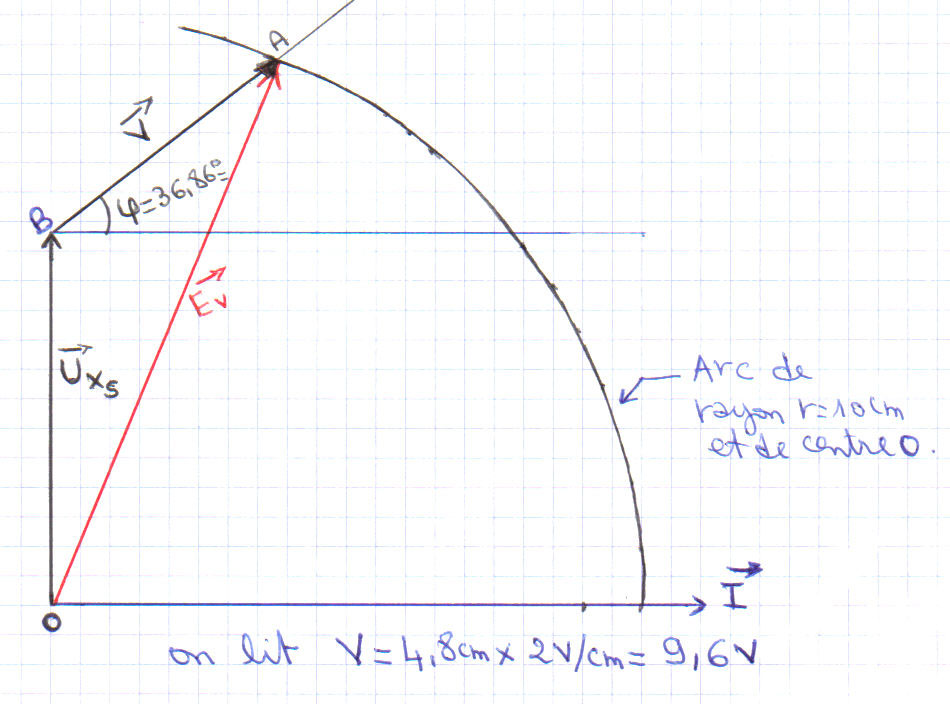
Construction vectorielle :
La charge est inductive et son facteur de puissance est 0,8 φ= cos-1 0,8 = 36,86° ( tension v(t) et en avance de 36,86° sur le courant d'induit i(t) ) on connaît donc la direction du vecteur
La tension uxs(t) aux bornes de l'inductance Xs est en avance sur l'intensité i(t) de 90°.
On connait le module de la f.é.m induite EV = 20 V , mais on connaît pas sa direction.
On prend une Echelle de 1cm pour 2V
a) On construit le vecteur UXS est en avance sur I de + 90°. ( longueur du vecteur 6,28 cm)
il faut ajouter le vecteur V à ce vecteur.
b) Le vecteur V fait un angle φ (qui est donné par cos-1( 0,80) = 36,86° ) avec le vecteur I .
On commence par tracer la droite support de ce vecteur ( en avance de 36,86° sur i(t)), mais nous connaissons pas sa longueur( c'est ce que nous cherchons).
mais on sais que la somme de ces deux vecteurs doit donner le vecteur EV dont nous connaissons la longueur (proportionnelle à 20 V, avec la même échelle).
c) Traçons un cercle de centre O et de rayon EV = 20 V (10 cm), il coupe la droite support du vecteur V en A.
 |
|---|
On trouve donc V = 9,6 V.
5) P = V.I cosφ = 9,6 x 8 x 0,8 = 62,4 W
6) h= Pu/Pa avec Pa = Pu + les pertes = 62,4 + 20 + 20 = 102,4 W h= 62,4 / 102,4 = 60,9 %.
Partie B
1)
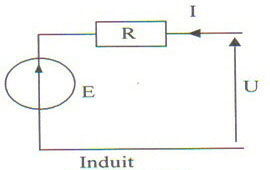
a) Le modèle équivalent de l'induit en régime établi :
 |
|---|
b) En appliquant la loi des mailles on a : U = E + R.I
2) Id = 40 A
a) A la mise en rotation du rotor Ω = 0 rad/s la F.ém induit E = 0 V.
b) U = R.Id = 0,2 x 40 = 8 V , la tension qu'il faut appliquer à l'induit au démarrage est U = 8 V.
3)
a) Ie = Ue / r = 48 / 20 = 2,4 A
b)
En charge la puissance absorbée par l'induit est : Pi = U.I = 48 x 30 = 1440 W.
La puissance absorbée par l'inducteur est Pe = Ue.Ie = 48 x 2,4 = 115,2 W
La puissance absorbée par le moteur est Pt = Pi + Pe = 1440 + 115,2 = 1555,2 W.
c) Les pertes Joules dans le moteur : pj = pjinduit + pjinducteur = R.I2 + r.I2e = 0.2 x 302 + 20 x 2,42 = 295,2 W
d)Pu = Pt - pj-pc= Pt - pj ( puisque on néglige les pertes autres que les pertes par effet Joules donc : les pertes collectives, pc= pfer + pmec = 0) .
Pu = 1555,2 - 295,2 = 1260 W
e) h =Pu/Pa= 1260 / 1555,2 = 0, 81 h =81%
f) Tu= Pu / W avecW= 2.Π.n/60 = 2 xΠx 800 / 60 = 83,73 rd/s
Tu=1260 / 83,73 = 15 N.m
g) E = U - R.I = 48 - 0,2x30 = 42 V
Partie C
1)
a) Le dispositif qui alimente l'induit du moteur est le HACHEUR.
b) On peut réaliser l'interrupteur K avec un Transistor ou un Thyristor.
c ) Le coefficient α est le rapport cyclique du hacheur, on le définit comme étant le rapport du temps de ferméture de l'interrupteur K sur la periode T du hacheur.
d) Le rôle de l'inductance L est de lisser le courant d'induit, afin que le moteur ni vibre pas à cause des variations du couple électromagnétique ( Tem = K.I).
e) La diode de roue libre D a pour rôle d'évacuer l'énergie stockée par l'inductance de lissage L quand l'interrupteur K s'ouvre.
2)
a )La valeur moyenne de uAB(t)est: <uAB> = AT / T = Vx.α..T / T =α . V
AT : L'aire sous la courbe uAB(t) sur la période T .
b) α .=<uAB> / V = 36 / 48 = 0,75