Accueil	Sujet

CORRECTION DU BTS MAI 2006

I-ETUDE DU PONT REDRESSEUR COMMANDE ( 4,5 points)

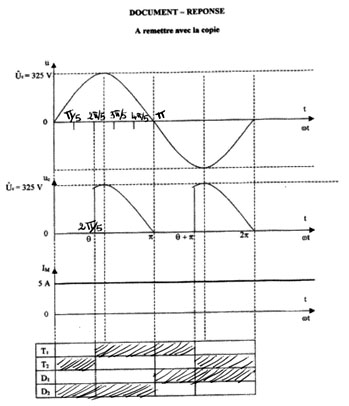
I-1: 0<θ<π on a la valeur moyenne de uc : <uc> = U_cmax( 1 + cos θ) / π.=325( 1 + cos θ) / π.=103.6( 1 + cos θ)

Pour θ= 0, ( cos 0 = 1) <uc> =207 V ;et pour θ= π ,( cos π = -1) <uc> =0 V. donc pour 0<θ<π on a 0 V < <uc> < 207 V .

I-2.

I-3. On lit sur le chronogramme de uc(t) un angle d'amorçage : θ= 2π/5= 72° dans ce cas <uc> = 325( 1 + cos 2π/5) / π.= 135,3 V .

I-4. On peut mesurer la valeur moyenne <uc> avec un simple voltmètre numérique en position DC.

II-ETUDE DU MOTEUR A COURANT CONTINU ( 8 points)

II-1.

Le thyrisor T1 conduit si u >0 et il y a présence d'une impulsion d'amorçage sur sa gachete.

Le thyrisor T2 conduit si u <0 et il y a présence d'une impulsion d'amorçage sur sa gachete.

La diode D2 conduit sur toute l'alternance positive ( u >0).

La diode D1 conduit sur toute l'alternance négative ( u <0).

II-2. D'après la courbe de la f.é.m E = f(Ω) de la figure 2 on a K représente la pente de cette courbe : K = E /Ω = 200 / 524 = 0,3817 V.rad^-1s.

II-3. E =U_M - R.I_M= K.Ω ce qui donne : Ω =(U_M - R.I_M )/ K

II-3.1 Application numérique: U_MN= 200 V et I_MN= 5 A .

Ω_N =(U_MN - R.I_MN )/ K = ( 200- 8x5)/0.3817 = 419 rad.s^-1.

II-4

II-4.1

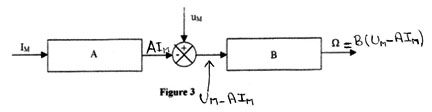
On a : Ω =(U_M - AI_M ).B= B.U_M - A.B.I_M

II-4.2 on a : Ω =U_M/K - I_MR/K= BU_M - A.B.I_M par identification des deux écritures on peut dire que : B =1 / K et A.B = R/ K (2)

Dans l'équation (2) on remplace B par /K on aura : A.x1/K = R/K ce qui fait que A = R.

B= 1/K = 1/ 0.3817= 2,62 rad s^-1 V^-1 et A = R = 8 Ω.

III-ETUDE DE L'ENSEMBLE ( MOTEUR MACHINE-OUTIL) ( 4 points)

-Toutes les pertes autres que par effet Joule sont négligeables. donc le moment du couple de pertes Tp = 0 N.m ce qui fait que Tem = Tu.

- Le moment du couple électromagnétique du moteur est de la forme: Tem =a.U_M - b.Ω avec a = 47,80.10^-3 NmV^-1 ;b= 18,24.10^-3 Nm rad^-1s ; Tem en Nm et Ω en rad s^-1.

-Le moment du couple résistant de la machine outil est : Tr = GΩ avec G= 4,56.10^-3 Nm rad^-1s ; Tr en Nm et Ω en rad s^-1.

III-1.Point de fonctionnement en régime permanent

On règle U_M à 200 V ;

III-1.1. on a Tem = a.U_M - b.Ω en régime permanent on a Tu = Tr donc Tr=GΩ sera égal à Tem.

GΩ=a.U_M - b.Ω ce qui fait que(G+b)Ω= a.U_M donc Ω = a.U_M / ( G+b)=47,80.10^-3 x200/ (4,56.10^-3 +18,24.10^-3 ) = 419,3 rad s^-1

Ω = 419,3 rad s^-1.

III-1.2. on a bien Tem = Tr car Tp= 0 N.m donc Tem =GΩ = 4,56.10^-3x 419,3 = 1,912 Nm.

III-2.Montée en vitesse du groupe

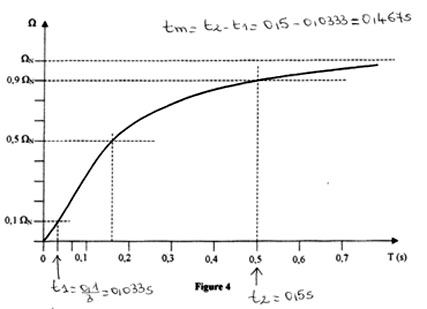
III-2.1. D'après le relevé du graphe de Ω en fonction du temps: on lit pour : à t = 0,033 s on a Ω(t) =0,1Ω_N ( 10 % de Ω_N)et t = 0,5 s on a Ω(t) =0,9Ω_N ( 90 % de Ω_N)

On en déduit que le temps de montée t_m qui est le temps mis par le groupe pour passer de 10 % à 90 % de Ω_N( valeur de Ω en régime permanent) est égal à :

t_m= 0,5 - 0,033 = 0,467 s.

III-2.2. La constante de temps mécanique τ_m est liée au temps de montée t_m par la relation : t_m = τ_mx ln(9) donc τ_m= t_m/ ln(9) = 0,467 / ln(9) = 212,4 ms.

τ_m= 212,4 ms.

IV-REGLAGE DE LA VITESSE DU GROUPE ( 3,5 points)

on désire une vitesse de rotation : Ω = 298 rad s^-1.

IV-1. on applique la loi des mailles au circuit d'induit de la figure 1 : u_c(t)=u_L(t)+u_M(t) en passant aux valeurs moyennes on a : <u_c>= <u_L>+<u_M>

Sachant que la valeur moyenne de la tension aux bornes de l'inductance est nulle <u_L>=0. donc <u_c>= <u_M>= U_M

IV-2

IV-2.1. En régime établi ona Tem =Tu= Tr ( car Tp = 0Nm) donc Tr = Tem = GΩ= 4,56.10^-3x 298 = 1,36 Nm.

A partir de la relation : Tem = a.U_M - b.Ω on calcule U_M = (Tem + bΩ)/a= (1.36 + 18,24.10^-3x298)/47,80.10^-3 = 142 V.

IV-2.2.Le nouvelle angle d'amorçage des thyristors se détermine à partir de la relation : <uc> = U_cmax( 1 + cos θ) / π.=325( 1 + cos θ) / π.=103.6( 1 + cos θ) = U_M .

U_M = 142 = 103.6( 1 + cos θ) donc 142 / 103,6 = 1 + cos θ =1,3733 ==> cos θ= 0,3733 et θ = cos^-1 (0,3733) = 68°.

θ = 68°.