| Page exercices | Retour à l'accueil |
|---|
Puissance en régime sinusoïdal
1) Puissance instantanée
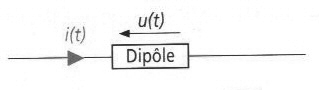
La puissance instantanée dissipée dans un dipôle linéaire, qui est soumis à une tension u(t) et parcouru par un courant i(t) est définie par la relation : p(t) = u(t).i(t) ( La puissance p(t) est une grandeur algébrique: elle peut être positive ou négative)
2) Puissance active dissipée un dipôle
La puissance active P dissipée dans un dipôle est égale à la valeur moyenne de la puissance instantanée p(t).
par définition : P= <p(t)> ( on lit valeur moyenne de p(t))
Soit un dipôle orienté en convention récepteur et soumis à une tension u(t) de valeur éfficace U et parcouru par un courant i(t) de valeur éfficace I.
|
|---|
Le dipôle introduit un déphasage φ entre les deux grandeurs électriques u(t) et i(t).
Les équations horaires de ces grandeurs sont données par :
u(t)= U√2 sinωt et i(t)= I√2sin(ωt-φ)
p(t)=u(t).i(t)=U√2.sinωt xI√2.sin(ωt-φ)
soit p(t) = 2.U.I sinωt xsin(ωt-φ)=2.U.I{(1/2) .cos (ωt- ωt+φ) - (1/2) . cos (ωt+ωt-φ)}
Finalement on a p(t) = U.I{cos (φ) - cos (2ωt-φ)}
la puissance instantanée est la somme de deux termes :
-Le premier terme : U.I cos φ est indépendant du temps t,
-le second terme : U.I cos (2ωt-φ) est une fonction sinusoïdale dont la variable est le temps donc sa valeur moyenne est nulle.
Finalement on dire que :
| P= U.I.cos φ |
|---|
P en watts,
U en Volts, et I en Ampères
La puissance active ne dépend que des valeurs éfficaces de l'intensité et de la tension et du déphasage existant entre ces deux grandeurs.
3) Puissance active pour les dipôles élémentaires
a) Résistance
Pour une résistance le déphasage φ=0 cos φ= 1 P= U.I =R.I2 = U2/R
une résistance reçoit de la puissance active.
b)Inductance pure
Pour une inductance pure l'intensité est en retard de 90° sur la tension, φ=90° cos φ=0. donc P = 0 W.
une inductance pure ne consomme pas de puissance active.
c)Condensateur
Pour un condensateur l'intensité est en avance de 90° sur la tension, φ= - 90° cos φ=0. donc P = 0 W.
un condensateur ne consomme pas de puissance active.
3) Puissance réactive
La puissance réactive est nécessaire à l'excitation magnétique ( la magnétisation) des récepteurs (Bobines, moteurs, transformateurs, ...).
On utilise la lettre Q pour désigner cette puissance, et elle est définie par la relation :
| Q= U.I.sin φ |
|---|
Q en En Volts Ampères Réactif (Var)
U en Volts, et I en Ampères
4) Puissance réactive pour les dipôles élémentaires
a) Résistance
Pour une résistance le déphasage φ=0 sin φ= 0 Q = 0 Var
une résistance ne reçoit pas de la puissance( énergie) réactive.
b)Inductance pure
Pour une inductance pure φ=90° sin φ=1. donc
 |
|---|
une inductance pure réçoit de la puissance réactive.
c)Condensateur
Pour un condensateur φ= - 90° cos φ=-1. donc
 |
|---|
un condensateur absorbe une puissance réactive négative .
5) Puissance apparente
Elle correspond au produit des valeurs efficaces de la tension et du courant et s'exprime conventionnellement pour la distinguer en VA (Volt-Ampère). Ce produit est apparemment une puissance mais ne fournit pas nécessairement un travail, d'où son nom de puissance apparente.
| S= U.I |
|---|
6) facteur de puissance
Ce paramètre (sans dimension) met en évidence la part utilisable de la puissance installée.
| Cos φ=P/S |
|---|
c'est un facteur important pour l'optimisation de la puissance à installer chez le client :
Un mauvais facteur de déphasage d'une installation entraîne de nombreux inconvénients :
une intensité en ligne plus élevée, provoquant des pertes Joule en ligne importantes.
des pénalités pour consommation excessive d'énergie réactive.
7)Triangle des puissances
Comme P= U.I.cos φ et Q= U.I.sin φ P2 + Q2 = U2.I2 ( cos2φ + sin2φ ) = (U.I)2= S2
 |
|---|
On peut écrire :
S=√(P2 + Q2) |
Q = P.Tan φ |
|---|
8. Représentation complexe des grandeurs électriques
Comme pour la représentation de Fresnel, le module est la valeur efficace U et l'argument la phase à l'origine θu .
| équation horaire | écriture exponentielle | écriture polaire |
|---|---|---|
u(t)= U√2 sin(ωt+θu) |
U=U.ejθu |
U =[U,θu] |
i(t)= I√2sin(ωt+θi) |
I=I.ejθi |
I =[I,θi] |
9. Puissances complexes
Soit la puissance apparente complexe: s =u .i* et développons ce produit:
s =U.ejθu .I.e-jθi=U.Iej(θu-θi)=U.Iejj=UI.cos φ + j.UIsin φ = P +jQ
φ =θu - θi représente le déphasage entre la tension u aux bornes du dipôle et le courant i absorbé par ce dipôle.
P =UI.cos φ: est la puissance active absorbée par un dipôle ( exprimée en W)
Q =UI.sinφ: est la puissance réactive absorbée par un dipôle (Exprimée en Var)
| s =P +jQ |
|---|