Exercices |
|---|
Modèle dynamique d'une machine à courant continu
On cherche à établir un modèle dynamique( fonction de transfert) de la machine à courant continu à excitation indépendante, la machine sera à flux constant .
On a donc deux relations de proportionalité entre la f.ém E et la vitesse du rotor : E= K. Ω , on a aussi un moment du couple électromagnétique directement proportionnel au courant d'induit : Tem = K.I
1) Equations Electromécanique du moteur à courant continu en régime dynamique
On modélise l'induit avec le modèle équivalent ci dessous, on tient compte de l'inductance L d'induit.
 |
|---|
a) Equations électriques
la tension d'induit ( en convention récepteur) : u(t)=R.i(t) + Ldi(t)/dt + e(t) (1) et la f.é.m : e(t) = K.Ω(t) (2)
R: résistance d'induit
L: inductance d'induit en henry
e(t): f.é.m induite
K: Constante tenant compte du flux constant
b)Equation mécaniques
Le principe fondamental de la dynamique (PFD)nous permet d'écrire :
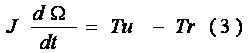 |
|---|
J: moment d'inertie de l'axe du rotor en Kg.m2
On a aussi Tu = Tem - Tp= K.I - Tp (4)
on suppose que le moment du couple résistant est de la forme : Tr = f .Ω (5)
f: coéfficient de frottement visqueux.
2) Equations électromécaniques dans le domaine de Laplace
La transformée de Laplace de l'équation (1) est : U(p) = R.I(p) + L.p.I(p) + E
La transformée de Laplace de l'équation (2) est : E = KΩ(p) (2'), on peut alors écrire : U(p) = (R.+ L.p)I(p) + KΩ(p) (1')
La transformée de Laplace de l'équation (3) est :Jp.Ω(p)= Tu - Tr = K.I - Tp - Tr= K.I - T'r (3')
et en tenant compte de l' équation (4) et (5) on peut écrire : Jp.Ω(p)= K.I - f.Ω(p) - Tp ![]() (J.p +f) .Ω(p)= K.I -Tp
(J.p +f) .Ω(p)= K.I -Tp ![]() Ω(p)= (KI-Tp)x1/(J.p +f) (4')
Ω(p)= (KI-Tp)x1/(J.p +f) (4')
3) Fonction de transfert du moteur
on suppose que le moment du coupe de pertes ( qui est vu comme une perturbation) est négligeable devant le moment du couple électromagnétique ce qui donne :
Ω(p)= KI/(J.p +f)![]() I(p) = Ω(p)(Jp +f)/ K et en remplaçant cette nouvelle éxpression de I(p) dans l'équation (1') on obtient :
I(p) = Ω(p)(Jp +f)/ K et en remplaçant cette nouvelle éxpression de I(p) dans l'équation (1') on obtient :
U(p) = (R.+ L.p)Ω(p)(Jp +f)/ K + KΩ(p)![]() U(p) = [(R.+ L.p)Ω(p)(Jp +f) + K2Ω(p)]/ K = [(R.+ L.p)(Jp +f) + K2]Ω(p)/ K on peut maintenant éxprimer la fonction de transfert en boucle fermée H(p) = Ω(p)/ U(p) :
U(p) = [(R.+ L.p)Ω(p)(Jp +f) + K2Ω(p)]/ K = [(R.+ L.p)(Jp +f) + K2]Ω(p)/ K on peut maintenant éxprimer la fonction de transfert en boucle fermée H(p) = Ω(p)/ U(p) :
 |
|---|
Qu'on peut écrire aussi sous la forme canonique d'une fonction de transfert de second ordre :
 |
|---|
avec τe = L/R et τ = R.J /( K2+ R.f)
K0 = K / (K2+ R.f) et α = R.f/ (K2+ R.f), on peut négliger α devant 1 : car K.I >> f Ω et aussi E = K.Ω >> RI
on aura une nouvelle écriture de la fonction de transfert :
 |
|---|
et si l'on a τe <<τ , c'est souvent le cas: la constante de temps électrique est négligeable devant la constante de temps électromécanique, on peut alors réecrire une nouvelle fois la fonction de transfert en factorisant son dénominateur: (τ +τe # τ on rajoute une quantité négligeable (τe) à τ)
 |
|---|
et on factorise à nouveau :
 |
|---|
C'est une fonction de transfert de second ordre de gain statique: K0 et qui a deux pôles ( négatifs donc stable) : -1/τ et -1/τe
 |
|---|